1. Basics of Graphing
By Marvin Roberts, BA, MPS, MPA
Graphs make it easier to see and understand economic relationships by turning complex data into clear visuals. They help economists identify trends, patterns, and how different variables relate to each other. This makes graphs useful for both understanding economic theories and making real-world decisions.
The Cartesian Plane
- Developed by René Descartes, the Cartesian plane is a powerful tool for visually representing the relationship between two variables.
- It is made up of two perpendicular axes:
- The horizontal axis (X-axis), which represents the independent variable
- The vertical axis (Y-axis), which represents the dependent variable
- The point where these axes intersect is called the origin, marked as (0, 0)
- The plane is divided into four quadrants, each defined by the signs of X and Y:
- Quadrant I: (+X, +Y)
- Quadrant II: (−X, +Y)
- Quadrant III: (−X, −Y)
- Quadrant IV: (+X, −Y)
- Every point on the plane is represented as a pair of coordinates (x, y), showing its position relative to the axes.
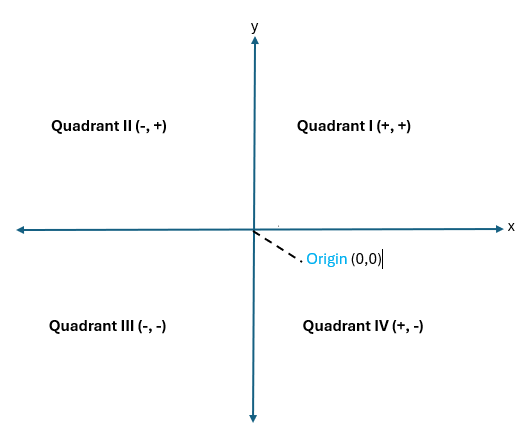
Understanding the Four Quadrants and Axes in the Coordinate Plane
-
Quadrant I:
-
Both the x- and y-coordinates are positive
-
This is the upper-right section of the coordinate plane
-
-
Quadrant II:
-
The x-coordinate is negative, while the y-coordinate is positive
-
This quadrant is located in the upper-left section
-
-
Quadrant III:
-
Both the x- and y-coordinates are negative
-
It represents the lower-left section of the plane
-
-
Quadrant IV:
-
The x-coordinate is positive, but the y-coordinate is negative
-
This is the lower-right section of the coordinate plane
-
-
Points on an axis:
-
Points that lie on the x-axis or y-axis (where one coordinate is zero) are not considered part of any quadrant
-
Coordinates of the form (x, 0) lie on the x-axis (horizontal)
-
Coordinates of the form (0, y) lie on the y-axis (vertical)
-

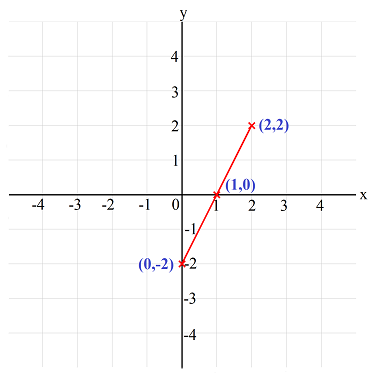

Slope
One way of describing the relationship between x and y or two variables is to use the slope of the line.
-
The slope of a line shows how one variable changes in response to another (rise over run)
-
A positive slope indicates a direct relationship (e.g., price ↑ → quantity supplied ↑)
-
A negative slope reflects an inverse relationship (e.g., price ↑ → quantity demanded ↓)

Positive Slope
A positive slope shows that as one variable increases, so does the other. In this case, as the number of hours studied increases, the test score also goes up. This is an illustration of a direct relationship.


The slope of 10 in this graph means that for every additional hour studied, a student’s test score increases by 10 points. This shows a positive, direct relationship between study time and performance—more hours of study lead to higher scores.